Condiciones de equilibrio
Las condiciones de equilibrio son las leyes que rigen la estática. La estática es la ciencia que estudia las fuerzas que se aplican a un cuerpo para describir un sistema en equilibrio. Diremos que un sistema está en equilibrio cuando los cuerpos que lo forman están en reposo, es decir, sin movimiento. Las fuerzas que se aplican sobre un cuerpo pueden ser de tres formas:
-Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.
-Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.
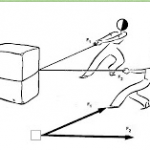
-Fuerzas colineales: Dos fuerzas son colineales cuando la recta de acción es la misma, aunque las fuerzas pueden estar en la misma dirección o en direcciones opuestas.
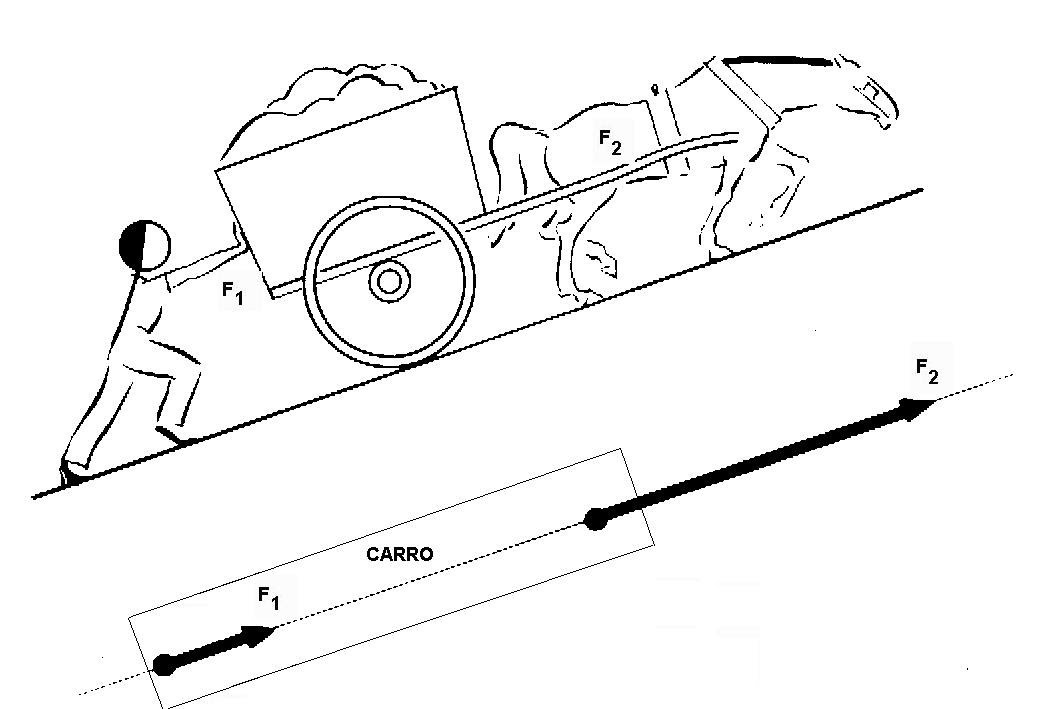

-Fuerzas paralelas: Dos fuerzas son paralelas cuando sus direcciones son paralelas, es decir, las rectas de acción son paralelas, pudiendo también aplicarse en la misma dirección o en sentido contrario.
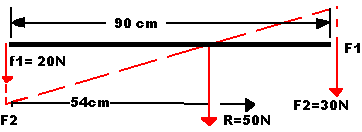
A nuestro alrededor podemos encontrar numerosos cuerpos que se encuentran en equilibrio. La explicación física para que esto ocurra se debe a las condiciones de equilibrio:

A nuestro alrededor podemos encontrar numerosos cuerpos que se encuentran en equilibrio. La explicación física para que esto ocurra se debe a las condiciones de equilibrio:
-Primera condición de equilibrio:Diremos que un cuerpo se encuentra en equilibrio de traslación cuando la fuerza resultante de todas las fuerzas que actúan sobre él es nula: ∑ F = 0.
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:
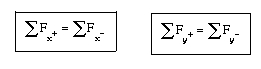
Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior, tal y como podemos observar en la siguiente imagen.
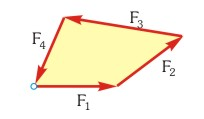
El hecho de que su gráfico corresponda a un polígono cerrado verifica que la fuerza resultante sea nula, ya que el origen de la primera fuerza (F1) coincide con el extremo de la última (F4).
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:

Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior, tal y como podemos observar en la siguiente imagen.

El hecho de que su gráfico corresponda a un polígono cerrado verifica que la fuerza resultante sea nula, ya que el origen de la primera fuerza (F1) coincide con el extremo de la última (F4).
-Segunda condición de equilibrio: Por otro lado, diremos que un cuerpo está en equilibrio de rotación cuando la suma de todas las fuerzas que se ejercen en él respecto a cualquier punto es nula. O dicho de otro modo, cuando la suma de los momentos de torsión es cero.
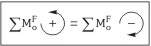
En este caso, desde el punto de vista matemático, y en el caso anterior en el que las fuerzas son coplanarias; se tiene que cumplir que la suma de los momentos o fuerzas asociados a las rotaciones antihorarias (en el sentido contrario de las agujas del reloj), tiene que ser igual a la suma aritmética de los momentos o fuerzas que están asociados a las rotaciones horarias (en el sentido de las agujas del reloj):
En este caso, desde el punto de vista matemático, y en el caso anterior en el que las fuerzas son coplanarias; se tiene que cumplir que la suma de los momentos o fuerzas asociados a las rotaciones antihorarias (en el sentido contrario de las agujas del reloj), tiene que ser igual a la suma aritmética de los momentos o fuerzas que están asociados a las rotaciones horarias (en el sentido de las agujas del reloj):
Un cuerpo se encuentra en equilibrio traslacional y rotacional cuando se verifiquen de forma simultánea las dos condiciones de equilibrio. Estas condiciones de equilibrio se convierten, gracias al álgebra vectorial, en un sistema de ecuaciones cuya solución será la solución de la condición del equilibrio.



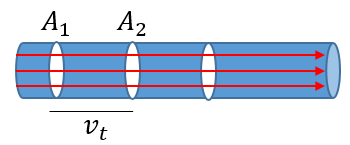
 ) es la magnitud física que expresa la variación de la masa con respecto al tiempo en un área específica. En el Sistema Internacional se mide en unidades de kilogramos por segundo, mientras que en el sistema anglosajón se mide en libras por segundo. Se usa frecuentemente en sistemas termodinámicos como tuberías, toberas, turbinas, compresores o difusores.
) es la magnitud física que expresa la variación de la masa con respecto al tiempo en un área específica. En el Sistema Internacional se mide en unidades de kilogramos por segundo, mientras que en el sistema anglosajón se mide en libras por segundo. Se usa frecuentemente en sistemas termodinámicos como tuberías, toberas, turbinas, compresores o difusores.














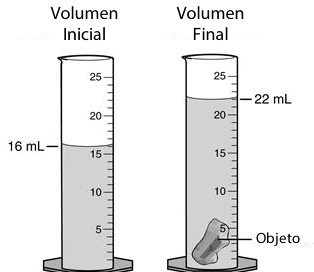









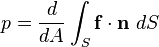
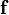 , es la fuerza por unidad de superficie.
, es la fuerza por unidad de superficie.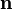 , es el vector normal a la superficie.
, es el vector normal a la superficie. , es el área total de la superficie S.
, es el área total de la superficie S.

